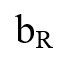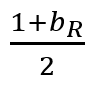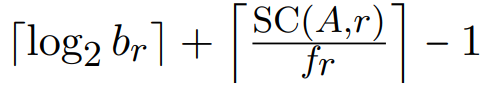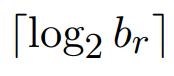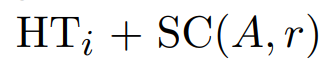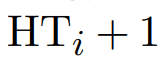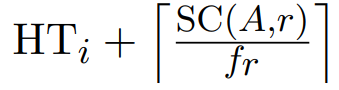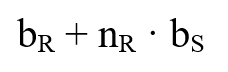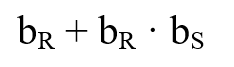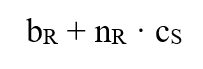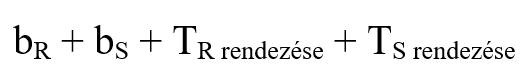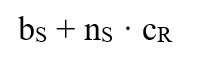Adatb - 4. gyakorlat

October 22, 2021

Elméleti összefoglaló

Hivatalos jegyzet/könyv: 6. fejezet ismerendő a gyakorlatra.

Előző alkalommal megismerkedtünk azzal, miként is szerveződik meg fizikai szinten az adatbázisunk. A fizikai adatbázisunk Fájlmenedzserét viszont most már nem fogjuk tovább vizsgálni. 🔬

Most egy okoskodós részéhez érünk a DBMS-nek: Visszatérünk a Lekérdezés feldolgozó egységhez, és annak a bonyolult belső működését fogjuk közelebbről megvizsgálni, ugyanis az optimalizáló algoritmusaitól fognak függeni leginkább a bonyolult lekérések visszatérésének idejei. ⛳️

A lekérdezés feldolgozása

Ezen paragrafus tulajdonképpen ismétlés, azonban most a Lekérdezésfeldolgozó modelljét finomítjuk, és újabb köztes munkafolyamatokat fogunk megismerni.

dbms

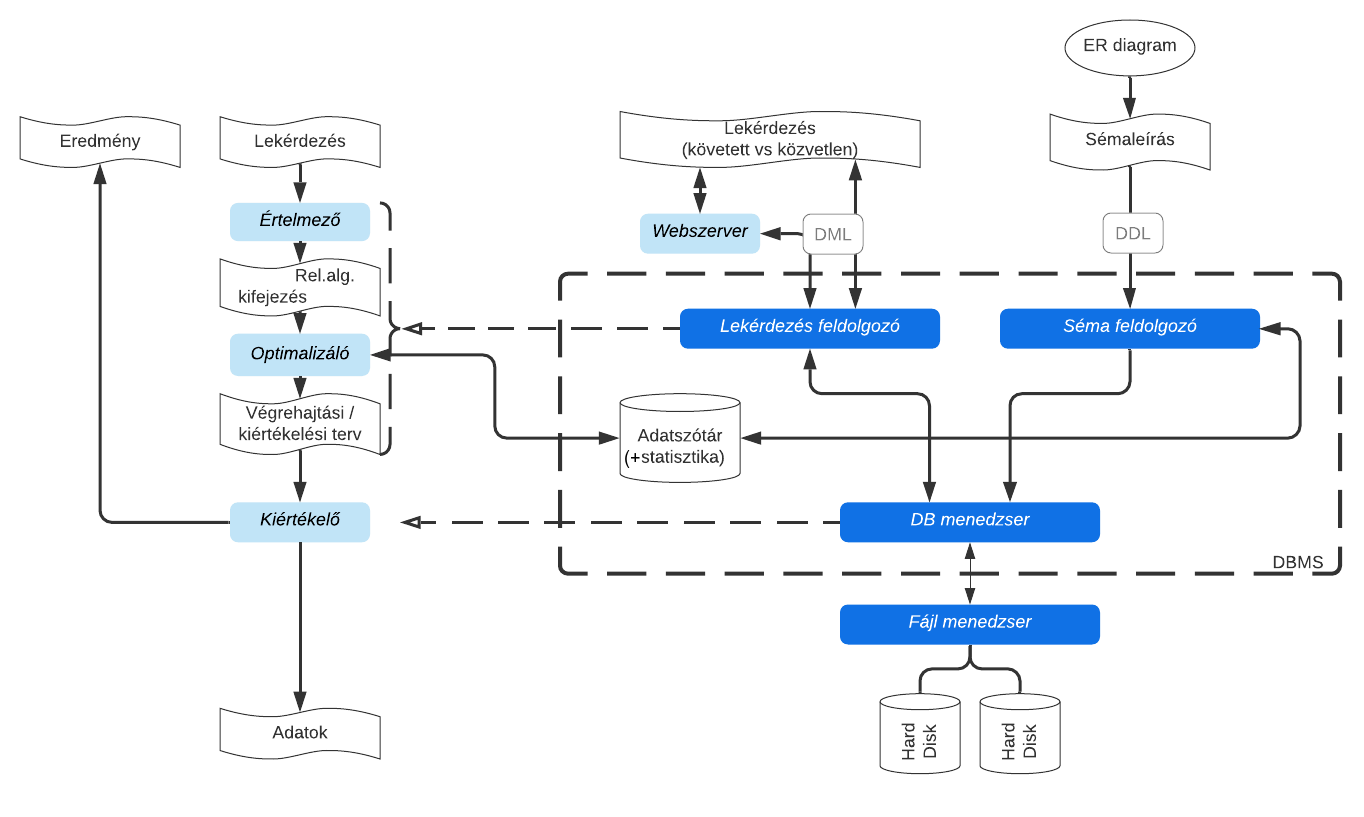
Oké: leküldjük a kalkulusban (tehát SQL-ben) megfogalmazott kérésünket a DBMS-nek, és a DBMS azzal kihalássza az adatállományból azt, ami nekünk kell. Arról viszont hajlamosak vagyunk megfeledkezni, hogy ez nem ebből a két lépésből áll, hanem:

a kalkulusból ugyanis először a feldolgozó fordít magának relációs algebrai kifejezést (ez a logikai műveletsorozat)
majd a relalg kifejezést okosan optimalizálja (erre különféle heurisztikákkal élhet, DBMS-e válogatja), azaz:
1. kiválasztja a megfelelő fizikai algoritmusokat a logikai műveletekre (pl.: joinok és szelekciók során hogy kezelje majd a végrehajtó modul a blokkokat)
2. meghatározza a legokosabb sorrendjét a logikai műveleteknek
3. végül az egészet munkafolyamatba teszi (materializáció és pipeline lehet ismert)
a fentiek eredménye egy végrehajtási terv, amelyet ki kell értékelni (van-e értelme azt választani), majd végrehajtani, azaz sorfordítani a logikai műveleteket fizikaira, azaz I/O műveletekre (pl.: READ, WRITE stb.)

Tehát így jutunk el a bonyolult SQL kifejezésünkből a sík egyszerű I/O műveletek soráig. Minket leginkább az érdekel, és azt szeretnénk megvizsgálni, hogy az optimalizálás során milyen algoritmusok, milyen munkafolyamatok léteznek, és általában milyen heurisztikával élnek a DBMS-ek, amikor újrasorrendezik a logikai műveleteket. Ezekről olvashatsz a tankönyvben is. A gyakorlat csupán a fizikai algoritmusokkal foglalkozik. 🧪

Adatszótár

Mi van az adatszótárban? Tulajdonképpen minden olyan handy dolog, ami jól jöhet a kiértékelés és optimalizálás elvégzéséhez: sokféle meta adatok. Többek között innen ismerhető meg egy-egy reláción az egyes oszlopokra mérhető Selection Cardinality (SC(A,r)), azaz hogy egy közönséges szelekciós lekérésnél (pl.: SELECT * FROM r WHERE A = 5;) várhatóan hány rekordot kaphatunk, valamint az oszlopban várhatóan hány különböző érték jelenhet meg (V(A,r)). Ezek alapján épül fel a költség-katalógus is!

Algoritmusok

Szelekció algoritmusai és azok lépésszámai

Fontos definíció mindenek előtt: Az elsődleges index olyan index, amely az indexrekordok olyan olvasását teszi lehetővé, hogy az olvasott sorrend megegyezik az adatblokkok tárolási sorrendjével -> Az adatállományban a rekordok éppen az A alapján vannak rendezve.

Az egyik kérdés az optimalizálásnál, hogy amikor egy szűrést alkalmazunk valamilyen attribútuma (nevezzük A-nak a keresési attribútumot) alapján egy relációra, akkor milyen algoritmust használhatunk a rekordok átkeresésére. Egy dolgot jegyezzünk meg még: általában a következő képlet segít kitalálni, mit kell számolni:

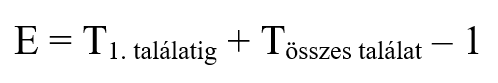
Tehát az átlag költséget legtöbbször az első találatig és az összes többi összegyűjtéséig tartó idővel számoljuk. Egy kérdezőfa segítségével vezetjük le a megfelelő és használható algoritmusok listáját.

Egyenlőség alapú szelekciók

Q: Van-e index a keresett attribútum alapján?
- A: Nem. → Q: Adatblokkok folyamatosan helyezkednek el ÉS a reláció A szerint rendezett?
  - A: Nem. Ekkor csak a lineáris keresést használhatjuk. → Q: Kulcs az attribútum, ami alapján keresünk?
    - A: Nem. Ekkor nem egyértelmű, hány találatunk lesz. Átlagosan az összes blokkot vizsgáljuk.
    - A: Igen. Ekkor egyértelmű, ha megvan az első találat, már végeztünk (hiszen unique a kulcs). Min: 1, Max: összes blokkot olvasnunk kell, átlagosan:
  - A: Igen. Ekkor a bináris keresést is használhatjuk. → Q: Kulcs az attribútum, ami alapján keresünk?
    - A: Nem. Ekkor a fenti átlag költség számolós képletet így alakíthatjuk át:
    - A: Igen. Ekkor az átlag költség egyszerűsödik:
- A: Igen. → Q: Elsődleges az index? (A szerint rendezett az adatállomány?)
  - A: Nem. (azaz másodlagos) → Q: Kulcs az attribútum, ami alapján keresünk?
    - A: Nem. Ekkor bizony alkalmazzuk szépen a fenti átlag költség képletünket. HTi az index szintszáma. Az első találat bizony HTi + 1 lesz, viszont itt nem osztunk a blocking factorral a többi találat megtalálására, mert mi van, ha a többi rekord más-más blokkokban vannak? Ehhez az első találattól jobbra lévő blokkokból Selection Cardinality darabszámú blokkot fogunk átlagosan megnézni még.
    - A: Igen. Úgyhogy akkor elég lemenni az első találatig. Vegyük észre, hogy a fenti képletben nincs ott a -1, viszont itt van egy +1, ennek indoka, hogy nem elég átmenni az index szintjein, utána még egy olvasás kell az adatállományból való kiolvasásra. Ezért is HTi + 1.
  - A: Igen. → Q: Kulcs az attribútum, ami alapján keresünk?
    - A: Nem. Ekkor bizony alkalmazzuk szépen a fenti átlag költség képletünket: (HTi az index szintszáma)
    - A: Igen. Ekkor viszont nincs szükség a többi elem megtalálására.

Összehasonlítás alapú szelekciók

Ez az ág nem könnyen magyarázható itt ilyen kérdés-válasz formában, inkább a könyv megfelelő fejezeteit kéne átolvasni. Itt is szóba jön, hogy elsődleges-e az index, vagy másodlagos...

Illesztés algoritmusai és azok lépésszámai

(Az egyes algoritmusok lépésszámánál feltételezzük, hogy a memóriába csak 1 blokk fér be)

Nested loop join
- Worst case:
- Egyik vagy mindkettő reláció elfér a memóriában:
Block nested loop join (feltéve, hogy 2 blokk is elfér a memóriában, külső ciklusban 1 blokkot beolvasunk, belsőben is 1 blokkot beolvasunk és utána ~0ms a CPU-val a memóriából összehasonlítgatni a blokkok rekordjait)
- Worst case:
- Egyik vagy mindkettő reláció elfér a memóriában:
Indexed nested loop join vagy
- Worst case: (c: itt az S reláción való indexelt szelekció átlag költsége)
- Egyik vagy mindkettő reláció elfér a memóriában:
Merge join
- Worst case:
- Már előre rendezve vannak a relációk:
Hash join
- Worst case: (c: itt az S reláción való hashelt szelekció átlag költsége)
- Egyik vagy mindkettő reláció elfér a memóriában:

Előjöhet az a gondolat a legtöbbjüknél, hogy mi van, ha nem csak 1-1 blokkot tudunk a memóriában tárolni a joinok során, ilyenkor pedig legtöbbjüknél a 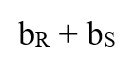képlet lehet használható. Hiszen gondoljunk csak bele, elég csupán beolvasni mindkét relációt egyszer a memóriába, utána akármilyen CPU műveletet végezhetünk velük, az ~0 millisecundumos idővel elvégezhető. 💡

Feladatsor

Forrás.

1. feladat: ismerkedés a jelölésekkel, katalógusinformációk, algoritmusok használata

Egy bank nyilvántartásában található, SZÁMLA(TELEPÜLÉS, EGYENLEG, ...) sémára illeszkedő relációból szeretnénk megtudni a budapesti számlák adatait. Ezeket tudjuk a relációról:

- fSZÁMLA = 40: SZÁMLA reláció 40 rekordja fér bele egy lemezblokkba.
- V (TELEPÜLÉS, SZÁMLA) = 50: 50 különböző fiók-név létezik a SZÁMLA relációban.
- V (EGYENLEG, SZÁMLA) = 500: 500 különböző értékű számla van a SZÁMLA relációban.
- nSZÁMLA = 10 000: A SZÁMLA relációnak 10 000 eleme van.

A feladat megoldása során tegyük fel, hogy a reláció elemeit optimális blokk-kihasználtság mellett tároljuk. Kérdések:

a) Adjuk meg a feladatot megoldó relációs algebrai lekérdezést!
b) Mennyi minimális/maximális/átlagos költség, ha lineáris keresést alkalmazunk? Mitől függ, hogy mennyi?
c) Tfh. a rekordok a fiók szerint rendezetten tárolódnak. Mennyi a bináris keresés várható költsége?

2. feladat: a join nagyságának becslése

Adott két relációs sémánk, a BANKBETÉT és az ÜGYFÉL. Illesszük a két (sémára illeszkedő) relációt a mindkettőben szereplő ÜGYFÉL_NÉV attribútum szerint, amely az ÜGYFÉL kulcsa, a BANKBETÉT-ben pedig idegen kulcs. Tegyük fel, hogy a két relációról a következő katalógusinformációk állnak rendelkezésre:

- nÜGYFÉL = 10 000
- fÜGYFÉL = 25 bÜGYFÉL = ?
- nBANKBETÉT = 5 000
- fBANKBETÉT = 50, bBANKBETÉT = ?
- V(ÜGYFÉL_NÉV, BANKBETÉT) = 2 500, SC(ÜGYFÉL_NÉV, BANKBETÉT) = ?

a) Hány olyan ügyfél van, akinek nincsen bankbetétje?
b) Mekkora a BANKBETÉT és az ÜGYFÉL természetes illesztésének mérete, ha egyetlen közös attribútumuk az ÜGYFÉL_NÉV?
c) Általánosítsuk a feladatot az alábbi esetekre (R és S az illesztendő relációk sémái, természetes illesztéssel)!
- c.a) R ∩ S = ∅.
- c.b) R ∩ S az R reláció kulcsa.
- c.c) R ∩ S ̸= ∅ egyik relációs sémának sem kulcsa.

3. feladat: hash join költsége

Számítsd ki a „hashjoin” algoritmussal végrehajtott join költségét, ha vödrös hashelést alkalmazunk! A hash függvény egyenletes eloszlással képezi le a kulcsokat az értékkészletére. Hogyan érdemes a join-t végrehajtani? A blokkméret nettó 2 000 bájt, a hashtábla szokás szerint elfér a memóriában.

R reláció: 120 000 rekord, rekordhossz 150 bájt, kulcs 12 bájt, mutató 8 bájt, a hash tábla mérete 10 000 bájt.
S reláció: 10 000 rekord, rekordhossz 250 bájt, kulcs 15 bájt, mutató 8 bájt a hash tábla mérete 1 000 bájt.

4. feladat: index-alapú illesztés

Számítsd ki az illesztés költségét, ha elsődleges, B*-fa struktúrájú indexeket használhatunk a join attribútumok szerinti rekordelérésre! A blokkméret nettó 4 000 bájt. Melyik reláció legyen a külső hurokban? Hányszoros válaszidőt kapunk, ha az optimalizáló rosszul dönt?

R reláció: 140 000 rekord, rekordhossz 140 bájt, kulcs 10 bájt, mutató 4 bájt.
S reláció: 15 000 rekord, rekordhossz 300 bájt, kulcs 6 bájt, mutató 4 bájt.

Házi feladat

Amire órán nem volt idő. Érdemes megnézni ZH előtt a tankönyv hátuljában lévő feladatokat, legtöbbjük elég jól felkészít a ZH-ban előkerülő dolgokra. Többször átnézni és megérteni, hogy melyik join algoritmus hány iterációt végez!

Ha találtok számotokra tetsző feladatot a könyvben, megoldjátok, elküldhetitek nekem a megoldásotokat, hogy rápillantsak, jónak tűnik-e. Ide emailezz: trisz@kir-dev.hu No stress.

Megoldások (ÚJ!)

4. feladat megoldása

Okosan ki tudjuk számolni blocking factor ésatöbbi segítségével azt, hogy

R reláció 5000 blokkból áll
S reláció 1154 blokkból áll

Valamint egy jólirányzott:

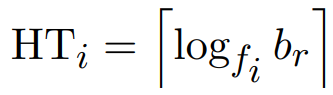
...képlet használával pedig kiszámolható, hogy 2 szintes lesz mindkét esetben a B*-fánk. Azaz minden rekordelérésnél 2 blokkot kell a B*-fából, és +1-et kell olvasni az adatblokkokból (összesen 3-at).

Ugyebár a fentiekből már ismerős lehet, hogyha indexelt illesztést használunk

R reláció a külső hurokban van, akkor képletünk a lenti lesz (végeredmény: 425000 lépés)
S reláció a külső hurokban van, akkor képletünk a lenti lesz (végeredmény: 46154 lépés, ő nyer)

Viszont ha az optimalizáló nem csak indexelt illesztést választhatna ezeken a relációkon, mi juthat eszünkbe? Vegyük figyelembe a feladat ezen mondatát: "...ha elsődleges, B*-fa struktúrájú indexeket használhatunk a join attribútumok szerinti rekordelérésre..." Hoppá! Hiszen elsődleges az index mindkét reláción ÉS (fontos hogy ÉS) az mindkét index éppenhogy az alapján az attribútum alapján épült, amit most a joinban is használunk!

Fordítsuk le magyarra mégegyszer: A join közös attribútuma legyen A. R reláción van egy B*-fa, aminek az A attribútum a keresési kulcsa. S reláción van egy B*-fa, aminek az A attribútum a keresési kulcsa. Mindkét B*-fa elsődleges index. Az elsődleges index definíciója pedig pontosan az, hogy az indexrekordok olyan olvasását teszi lehetővé, hogy az olvasott sorrend megegyezik az adatblokkok tárolási sorrendjével -> Az adatállományban a rekordok éppen az A alapján vannak rendezve.

Emeljük ki a tényt, hogy rendezett az adatállományunk. Ez a tény lehetőséget ad arra, hogy merge join-t (összefésüléses illesztést) használjunk az indexeltek helyett! 🎊 🎉

Merge join esetén pedig a képletünk sokkal egyszerűbb lesz, csupán a két reláció blokkjainak számát kell összeadnunk (végeredmény: 6154 lépés, ő nyer végül), hiszen a fésüléses join csak megyeget a blokkokon és fésülgeti őket, ha van egyezés A attribútum alapján.