Adatb - 3. gyakorlat

Elméleti összefoglaló

Hivatalos jegyzet/könyv: 3. fejezet ismerendő a gyakorlatra.

Előző alkalommal megismerkedtünk azzal, milyen nyelveken tudunk lekérést intézni az adatbázisok felé. A parancsaink megérkeznek a Lekérdezés feldolgozóba, majd a DB menedzser sok okoskodás után (amit még később ismerünk csak meg) leadja a "rendelést" a fizikai adatbázisunk fájl menedzserének.

Ekkor egy kritikus részéhez érünk DBMS-nek: ugyanis a fizikai adatbázisunk fizikai szervezésétől fog függeni leginkább a lekérésünk visszatérésének gyorsasága. Amilyen adatstruktúrákat és algoritmusokat itt alkalmazunk, az fogja leginkább meghatározni azt, mennyi ideig tart egy átlagos lekérés.

Blokkok

Az adatbázisokban kevés CPU-igényes és kevés memória-igényes feladatunk van. Sokkal inkább I/O-igényes feladataink vannak. Tehát mivel Számítógéparchitektúrák tárgyból már megismerhettetétek, hogy a hardveres világban amikor egy szoftver I/O műveletet hajt végre - azaz a merevlemezen olvas/ír -, akkor a hardveren történő 1 blokkművelet átlagos ideje számít, a többi idő elenyésző.

Éppen ezért leszünk mi is kíváncsiak a blokkműveletek számára, amikor az adatbázisunk fizikai adatszervezését tervezzük. Nézzük is meg, hogy mi van egy blokkban:

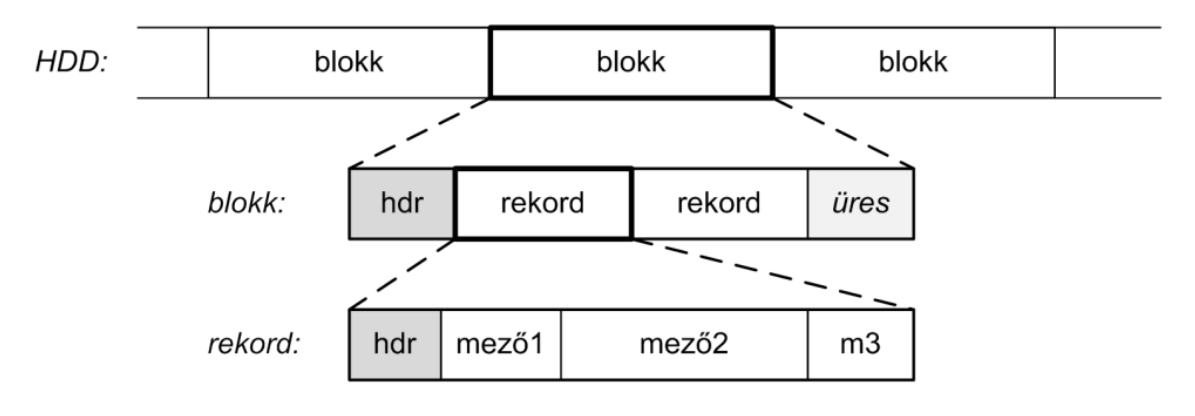
Röviden ami nekünk fontos ebből:

• Blokk az alapvető műveleti egység: Lekérdezéskor blokkokat fogunk beolvasni a memóriába és onnan visszaírni a lemezre.
• 1-1 blokkban több rekord is lesz - azaz a relációink egyes sorai.

Néhány fontosabb jelölés és számolás:

Blokkok szervezése

Amit ezen a gyakorlaton ismerhettek meg - adatszervezési modellek, azokra kitalált algoritmusok - két későbbi 4. féléves tárgyatok fogja még részletesebben bemutatni: Algoritmuselmélet és Operációs rendszerek. Szóval no worries, ha valaki kevésnek tartaná az itt megismert dolgok halmazát, ő még később több ismeretre fog szert tenni adatszerkezetekkel és algoritmusaikkal kapcsolatosan. Mi csupán a leggyakoribb adatszerkezeteket és azok egyszerűbb működési algoritmusait fogjuk tárgyalni.

Heap

Fontos: A heap itt a szó szerinti halom értelmében értelmezendő -> azaz a heap egy halom adat egymásracsapva, ahogy jönnek. Semmi rendezettség, semmi logika.

Nem összekeverendő a Heap fa adatszerkezettel, amelyet a roppant hatékony komplexitású heapsort rendezési algoritmus is használ.

Vödrös hash

A vödrös hash megnöveli az adatok rendezettségét: nem egy nagy halomba tesszük az adatokat, hanem több "vödörbe". Létrehozunk egy h(k): K -> [0 ... B-1] alakú leképezési függvényt. Például lehet ennek a definiálása valami c konstans mellett: h(k) = (c * k) mod B, ahol a k a keresési kulcs, amit átadunk a leképezési függvénynek (ez lehet pl. egy könyv sorozatszáma és ekkor a sorozatszám vödrökkel vett maradékos osztásának eredménye alapján osztjuk be az elemeket a vödrökbe).

Indexek

Az indexek tulajdonképpen csupán egy újabb absztrakciós szintet tesznek a valódi adatblokkok fölé. Ez egyáltalán nem rokona a hashnek! A hashben függvény segít nekünk az adatállományban megtalálni a keresett elemet. Az index viszont NEM függvény, ez egy segédstruktúraként szolgáló valódi adathalmaz! Itt is vannak blokkok és rekordok.

Nevezzük az adatállományt D-nek, az indexállományt I-nek. Ekkor:

• D-ben: egy adatblokk tartalmaz több adatrekordot.
• D-ben: egy adatrekord tartalmazza a rekordhoz tartozó mezőknek értékeit.
• I-ben: egy indexblokk tartalmaz több indexrekordot. -> Mikre képezzük az indexrekordokat❓
• I-ben: egy indexrekord tartalmaz egy keresési kulcsértéket (pl.: könyvcím) és egy mutatót. -> Mire mutat a mutató❓

Fontos: Az indexállományt mindig rendezve tartjuk! Mit jelent ez? A két indexelési formánál külön-külön kap ez a mondat értelmet, lássuk...

Ritka index

Q: Mikre képezzük az indexrekordokat?

A: Ritka index esetén az indexrekordokat egy-egy adatblokkra képezzük. Ilyenkor az indexrekordban található keresési kulcsérték (pl.: könyvcím) értelme bonyolódik. Legyen 2 egymásmelletti indexrekordunk: Micimackó, aztán utána Mulan. Oké, de hol van a Mikiegér kalandjai című könyv? Az indexrekordok között nincs ilyen! Pedig az adatrekordok között van ilyen könyv.

Akkor viszont ez egy dolgot jelenthet: A Micimackó indexrekordja nemcsak a Micimackó adatrekordra fog leképeződni, hanem minden más adatrekordra is, ami még a Mulan előtt van! Tehát az indexrekordok keresési kulcsa egy intervallum kezdetét fogja mutatni.

Megesik, hogy az indexrekordok keresési kulcsa NEM az intervallum kezdetét fogja leképezni, hanem a végét. Azonban mi most a tárgy keretében olyan ritka indexeket fogunk építeni, amik az intervallumok kezdetére képződnek.

Tehát így hány darab indexrekordunk lesz? Amennyi adatblokk van.

Q: Mire mutat a mutató?

A: Egy indexrekordban a mutató mutat arra a teljes adatblokkra, amiben az az adatrekord van, amire kerestünk. Fentebb kifejtettük, milyen másik adatrekordok lesznek még a mutatott adatblokkban. Lejjebb kifejtetjük, hogy ez mit jelent az index rendezettségének szempontjából.

Q: Az indexállományt mindig rendezve tartjuk! Mit jelent ez a ritka index esetén?

A: Ritka index esetén muszáj az indexrekordokat úgy tárolni, hogy azok valamilyen sorrendben legyenek, pl.: betűrendben, ha könyvcímekről beszélünk. Így lesz elég könnyű keresgélni az adatrekordokon pl.: bináris kereséssel (ami nagyon gyors).

🚀 Valamint fontos belegondolni: Legyen 2 egymásmelletti indexrekordunk: Micimackó, aztán utána Mulan. A Micimackós indexrekord egy egész adatblokkra mutat, a Mulanos egy másikra. Ezért a Micimackós adatblokkon BELÜL csak olyan adatrekordok lehetnek, amik között ott van a Micimackó és minden olyan könyv rekordja, aminek a címe még megelőzi a Mulant! Ugyanis a Mulan már egy másik adatblokkban van. Tehát a ritka index esetén az adatblokkokon belül az adatrekordok intervallumrendezettek. Ez nem jelenti, hogy az adatblokkon belül betűrendben vannak az adatrekordok, de az biztos, hogy egy bizonyos intervallumon belüliek ezek a rekordok.

B*-fa

A ritka index alfaja. Több szintű ritka index igazából, de azt okosan kialakítva:

1. Legalsó szinten úgy működik mint egy egyszerű ritka index: egy-egy indexrekord egy-egy adatblokkra képeződik.
2. Ezeket az alsó szinten lévő indexrekordokat indexblokkokba csomagoljuk.
3. A felette lévő szinten most már egy-egy indexrekord egy-egy indexblokkra fog képeződni.
4. Visszatérünk a 2. lépésre rekurzívan, és lépegetünk felfelé, építjük a szinteket.

STOP: Akkor állunk meg, amikor a legfelső szint már csak 1 db indexblokkból áll.

A számolásokat mindenképp nézzétek meg újra a könyvben gyakorlat után is, de a gyakorlaton remélhetőleg mindenképp értelmet fognak nyerni!

Sűrű index

Q: Mikre képezzük az indexrekordokat?

A: Sűrű index esetén az indexrekordokat egy-egy adatrekordra képezzük. Ilyenkor az indexrekordban található keresési kulcsérték (pl.: könyvcím) értelme egyértelmű. A Micimackó indexrekordja a Micimackós adatrekordra fog leképeződni.

Tehát így hány darab indexrekordunk lesz? Amennyi adatrekord van.

Q: Mire mutat a mutató?

A: Egy indexrekordban a mutató mutat arra a teljes adatblokkra, amiben az az adatrekord van. HOPPÁ!!! Ez ugyanaz, mint a ritka indexnél! Egyetlen indoka van: mutathatnánk csak a rekordra is, de amúgyis a kiolvasáskor egy egész adatblokkot tudunk csak kiolvasni, nem egy kis adatrekordot, így akkor már muszáj az adatblokkra mutatni. Viszont fontos különbség, amit tényleg érdemes kiemelni: Minden adatrekordra van egy-egy indexrekord, nem csak a blokkokra!

💡 Pont emiatt a sűrű index önmagában nem elég. A sűrű indexre mindig ráépül egy másik adatszervezési paradigma: ritka index vagy hash. A sűrű indexek elsősorban a fő állomány kezelését könnyítik meg, illetve a több kulcs szerinti keresést teszik lehetővé.

Q: Az indexállományt mindig rendezve tartjuk! Mit jelent ez a sűrű index esetén?

A: Sűrű index esetén muszáj az indexrekordokat úgy tárolni, hogy azok valamilyen sorrendben legyenek, pl.: betűrendben, ha könyvcímekről beszélünk. Így lesz elég könnyű keresgélni az adatrekordokon pl.: bináris kereséssel (ami nagyon gyors).

Viszont itt már nem kell semmiféle rendezettséget elvárni az adatállománytól! Már nem intervallumokat jellemeznek az indexrekordok, hanem konkrét adatrekordokat! Sőt, tök jó, mert a sűrű index meggyorsíthatja a rekordelérést, hiszen ha csapunk fölé egy ritka indexet, akkor annak a mérete jóval kisebb is lehet, mint egy sűrű nélküli ritka index! 🏖

Vegyesfelvágott

Segítsünk, hogy a fenti megállapítás - 💡 a sűrű indexek a több kulcs szerinti keresést teszik lehetővé - értelmet nyerjen!

Házi feladatként feladom a könyv 225. oldalán található Fizikai szervezés témakörében feladott 33-as feladatot. A megoldása a 242. oldalon kezdődik és gyakorlatiasan megérthető a két kulcs szerinti keresés működése indexekkel (méghozzá a B*-fával egy egészen elegáns megoldást kapunk a problémára).

Kitekintés

Ha a kisujjadban van a fizikai architektúrák ismerete, és unalmas lenne számodra ez az anyagrész, és szívesebben foglalkoznál magasabb absztrakciós/szoftveres szintjeivel az adatbázisoknak, akkor ajánlom megtekintésre ezt a Youtube playlistet: youtube.com/playlist?list=PLOspHqNVtKAAXDobTc9kBWwnfgzNV2k_a az IBM-től, amelyben a cloud alapú adattárolás iparban is széles körben felhasznált technológiáit mutatják be.

Feladatsor

Forrás.

1. Egy 1000 rekordból álló állományt ritka index szervezéssel tárolunk. A rekordhossz 850 bájt, egy blokk kapacitása (a fejrészt nem számítva) 4000 bájt. A kulcs 50 bájtos, egy mutatóhoz 18 bájt kell.

• a) Hány rekord fér el egy blokkban?
• b) Hány blokkot foglal el az indexstruktúra és mennyit a teljes állomány?
• c) Melyik szinten, melyik blokkokban és blokkok között követeljük meg a rendezettséget?
• d) Mennyi ideig tart legfeljebb egy rekord tartalmának kiolvasása, ha feltételezzük, hogy az index struktúra már benne van az operatív tárban? (egy blokkművelet ideje 5 ms)
• e) Mennyi ideig tart legfeljebb egy rekord tartalmának kiolvasása, ha az index struktúra nem fér el az operatív tárban? (egy blokkművelet ideje 5 ms)

2. Egy 7 vödörrel rendelkező hash tábla leképező függvénye h(k) = k mod B. A következő rekordok érkeznek, amelyeket szeretnénk eltárolni: 56, 91, 27, 19, 36, 52, 79.

• a) Feltételezve, hogy egy rekord egy blokknyi méretű, mennyi az átlagos rekordelérési idő?
• b) Tetszőleges másik hash függvényeket választva mennyi az elméletileg elérhető legjobb és legrosszabb véletlenszerű rekordelérési idő ugyanekkora elemszámnál?

3. Vödrös hash szervezéssel tárolunk egy állományt, amelyben a rekordok száma 15000. Egy rekord hossza 120 bájt, egy blokkba 4000 bájt fér el, egy kulcs hossza 25 bájt, egy mutatóé 8 bájt. A szervezést 10 vödörrel oldjuk meg. (Feltételezhetjük, hogy a hash függvény egyenletesen osztja el a kulcsokat.)

• a) Mekkora az átlagos vödörméret?
• b) Mekkora lemezterület szükséges a teljes struktúra tárolásához (valódi méret, illetve felhasznált tárterület)?
• c) Mennyi az átlagos rekordelérési idő, ha a blokkelérési idő 5 ms? (A keresés során a vödör-katalógust a memóriában tároljuk.)
• d) Mekkora legyen a vödrök minimális száma, ha a keresés során átlagosan 5 blokkelérési idő alatt akarjuk megtalálni a keresett rekordot?

4. Egy állományt kétféle szervezéssel tudunk tárolni: sűrű index, majd erre épített egyszintes ritka index vagy pedig hash algoritmussal. Az állományon néha intervallumkeresést is meg kell valósítani. Melyik szervezési módszert válasszuk? Adjon értelmes alsó becslést a szükséges blokkok számára az alábbi feltételek mellett:

• az állomány 3 000 000 rekordból áll
• egy rekord hossza 300 bájt
• egy blokk mérete 4000 bájt
• a kulcshossz 45 bájt
• egy mutató hossza 5 bájt

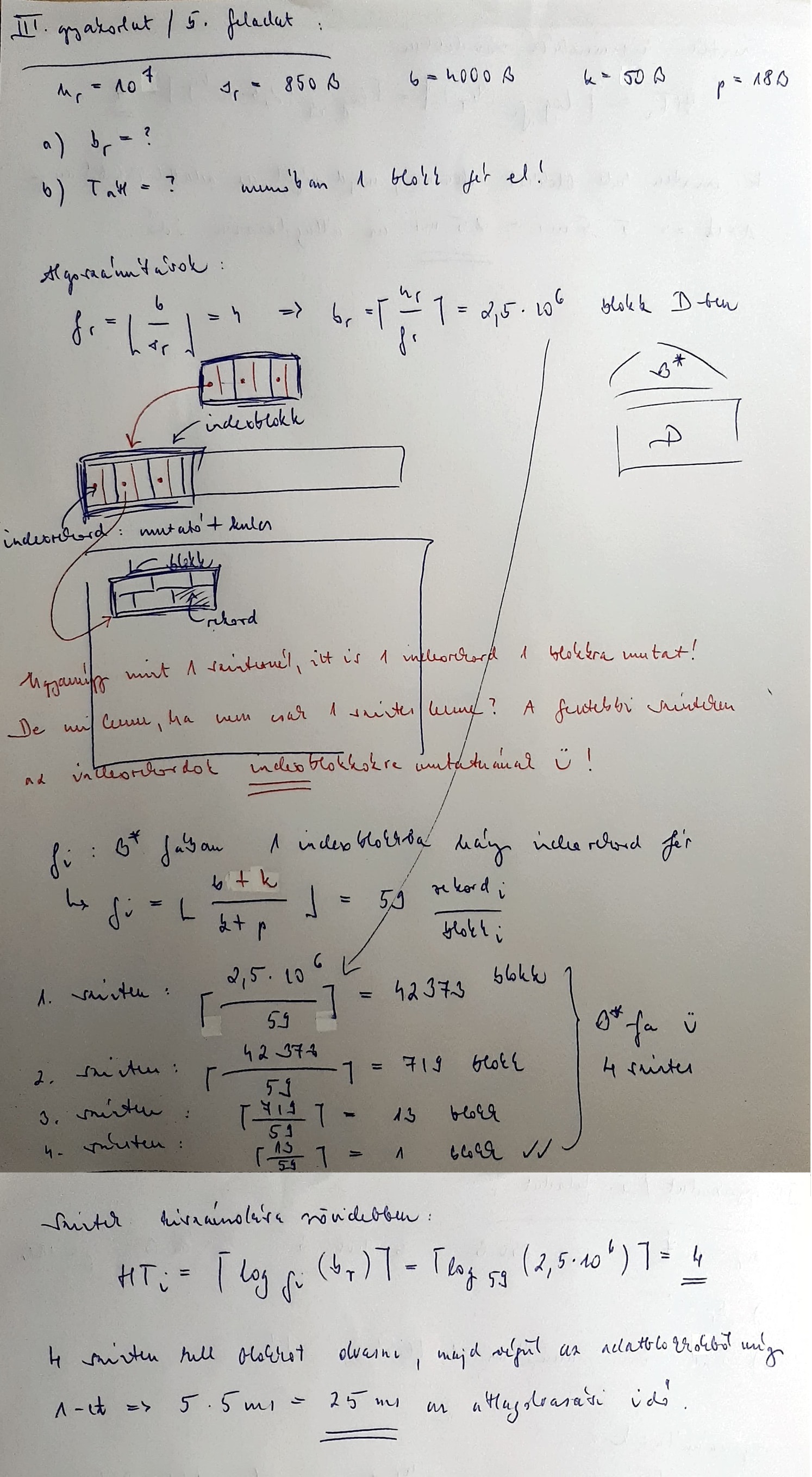
5. Egy 10 000 000 rekordból álló állományt szeretnénk B*-fa szervezéssel tárolni. A rekordhossz 850 bájt, egy blokk kapacitása (a fejrészt nem számítva) 4000 bájt. A kulcs 50 bájtos, egy mutató tárolásához 18 bájt kell. Legalább hány blokkra van szükség? Mennyi az átlagos rekordelérési idő, ha a memóriában egy blokk fér el? (Egy blokk elérésének ideje 5 ms.)

Házi feladat

Amire órán nem volt idő. Érdemes megnézni ZH előtt a tankönyv hátuljában lévő feladatokat, legtöbbjük elég jól felkészít a ZH-ban előkerülő dolgokra. Valamint érdemes a sűrű + ritka index kombinációk előnyein és hátrányain komolyan elgondolkodni (több keresési kulcs alapján történő keresés, okos adatszervezés).

Ha találtok számotokra tetsző feladatot a könyvben, megoldjátok, elküldhetitek nekem a megoldásotokat, hogy rápillantsak, jónak tűnik-e. Ide emailezz: trisz@kir-dev.hu No stress.

Megoldások (ÚJ!)

5. feladat megoldása