Adatb - 2. gyakorlat
Elméleti összefoglaló
Hivatalos jegyzet/könyv: 5.1-5.3 alfejezetek ismerendőek a gyakorlatra.
Építsünk az előző heti gyakorlat elméleti összefoglalójára. Eddig ugyebár idézőjeles "adatmodellként" csak az ER modellel ismerkedhettünk meg, de - mint tudjuk - mivel nem lehet műveleteket végezni rajtuk, nem a legjobb ötlet ezekből adatbázis rendszereket készíteni. Hiszen - ahogy egy DBMS-től elvárható - szeretnénk tudni az adatokon és struktúrákon műveleteket végezni: írni + olvasni + módosítani + törölni (CRUD).
A következőkben megismerkedünk a relációs adatmodellel, és annak 3 matematikai paradigmájával, amelyekkel műveleteket tudunk definiálni rajtuk: relációs algebra vs. sorkalkulus vs. oszlopkalkulus. (ajánlott rövidítések: "relalg", "sorkalk", "okalk")
Relációk
Definíció: Halmazok Descartes-szorzatának részhalmaza.
- A sorok sorrendje sosem számít!
- Kardinalitás: Az egyes oszlopok/attribútumok különböző értékeinek száma
- Aritás / Reláció foka: A relációban lévő oszlopok/attribútumok száma
- Reláció számossága: A relációban lévő sorok száma (a konkrét előfordulások száma!)
- Relációs séma: melyik relációban milyen attribútumok találhatók (nagybetűs
R)- Egy-egy relációs sémára épülhet több reláció (kisbetűs
r)
- Egy-egy relációs sémára épülhet több reláció (kisbetűs
- Adatbázis séma: egy adatbázis relációs sémáinak összessége
Műveletek relációkkal
Deklaratív vs. Imperatív programozás
A két programozási paradigma elveikben különböznek, de mindkettőnek egy a célja: kommunikálni a számítógép felé, hogy az majd nekünk szépen előállítsa az eredményt - amit mi nagyon szeretnénk.
Különböznek abban, hogy különféleképp tudnak kommunikálni a számítógéppel. Éppen emiatt azzal a nehézséggel járnak, hogy különböző gondolkodási módszert kell alkalmaznunk emberként, amikor valamelyik paradigmát alkalmazva akarjuk a számítógépet eredménygenerálásra bírni.
Deklaratív: Nem érdekli, hogy a számítógép saját maga milyen lépésekben fogja végrehajtani a dolgokat a háttérben, csupán annyit kommunikál le a számítógép felé, hogy milyen formában, milyen feltételekkel kéri az eredményeket az adathalmazokból. Tehát ez az igényközlő, passzív-agresszív módszer, azaz a matekozós-logikázós gondolkodást igénylő módszer. 🤔
Imperatív: Őt már érdekli, hogy milyen lépéseket akarsz neki betáplálni ahhoz, hogy ő dolgozzon az adatokkal. Azt kommunikálod le ezzel a paradigmával, hogy explicite milyen lépéseket hajtson végre az adaton a számítógép. Ezzel találkozhattatok már, amikor Assemblyben, C/C++-ban vagy Javaban programoztatok. 🤖
Relációs algebra
Ez az imperatív megközelítés! Érdemes halmazként kezelni a relációkat (ahogy definiáltuk is), azonban okosan, mert muszáj jól definiálni hozzájuk a halmazműveleteket, hiszen butaság volna komplementert kitalálni a relációkra (az ilyen végtelen ismeretlen vacak volna).
Alapműveletek:
- Unió
- Különbség
- Descartes-szorzat
- Projekció/Vetítés (pi)
- Szelekció/Szűrés (szigma)
Ezekkel fent már teljes lekérdezőnyelvvé is vált a relalg, de lehet persze származtatott műveleteket adni neki:
- Természetes illesztés (most csak ezt fogjuk használni egyedül)
- Théta-illesztés
- Hányados
Sor- és oszlopkalkulus
Tehát ő lesz az egyik deklaratív megközelítés, egyben a logikai megközelítés. Tehát alkalmazzuk a matematikai logikát, amikor a kalkulusokkal foglalkozunk. Miből épül fel egy logikai/kalkulus kifejezés?
szimbólumok -> atomok -> formulák -> kifejezések
Mi a gyakorlaton majd megpróbálunk ügyes formulákat kifejleszteni, amelyekből a feladatnak megfelelő kifejezéseket alakíthatunk. Tehát megpróbálunk tipikus formula-trükköket megismerni. 💡
Fontos: okosan kell formalizálnunk a kifejezéseink, hiszen a kalkulus sokkal nagyobb szabadságú világgal rendelkezik -> csak az interpretációs halmaz adja neki a határt (ami lehet végtelen számosságú!).
Meg kell nézzük a formuláink doménjeit, ugyanis ha már biztonságos a kifejezésünk, akkor már boldogabbak lehetünk (visszatérünk a véges számosság világába). Ha számosság világában vagyunk, annak örülünk, hiszen így a kalkulus-kifejezés kiértékelhető lesz számítógépben kezelhető méretű relációk/véges idő mellett is. ✔️
Formula doménje: DOM(phi) = { phi-beli relációk attribútumainak értékei } + { phi-beli konstansok }
Biztonságos { t | phi(t) } kifejezés:
- A
t-k, amik aphi(t)-t kielégítik, azoknak mindnek az attribútumértékei DOM(phi)-beliek. - A
phi(t)-n belüli(∃u)({ u-val dolgozó részformula })alakú részformulák biztonságosak (rekurzió)
Kitekintés
A megismert 3 matematikai paradigma segítségével szoktak DBMS tervezők lekérdező nyelveket definiálni az adatbázisok szoftveres világában. Ezen lekérdező nyelvek segítségével tud a programozó egyértelmű lekéréseket írni, amit majd a Lekérdezés feldolgozó fog értelmezni és abból az eredményt visszaadni.
Egy ilyen ismert lekérdezési nyelv az SQL, amelyről már az előző posztban is egy keveset írtam. Az SQL egy tipikus deklaratív programozási nyelv - ötvözi az sorkalkulust és (nagyobb részt) az oszlopkalkulust. Ezt majd saját magatok is tapasztaljátok a laborokon. Általában a relációs DBMS-ek az SQL-t használják lekérdezési nyelvükként, azonban legtöbbjük saját dialektust talál ki a saját DBMS-ének kiszolgálására - a dialektus itt értelmezhető akár úgy, mint ahogy a természetes nyelvek körében szoktuk értelmezni: nyelvváltozat, kicsit személyre szabva a DBMS különleges funkcióinak ellátására.

Ilyen dialektus a PLSQL is, amelyet az Oracle talált ki a saját DBMS-éhez is - amellyel kicsit majd a laborokon is meg fogtok tudni ismerkedni, nem túl részletekbe menően. Ennek a dialektusnak a lényege, hogy az SQL meglévő tudásához hozzáadja a "procedúrák", azaz eljárások lehetőségét is. Ezáltal a PLSQL nemcsak deklaratív programozási lehetőségekkel szolgál, hanem imperatívakkal is.
A deklaratív programozáshoz tartozik pár érdekesebb ma is használt programozási nyelv az SQL-en kívül pl. Elixir, Prolog, Erlang vagy Haskell.
A relációs adatbázisokkal kapcsolatban ajánlom az IBM rövid ismeretterjesztő videóit: youtube.com/watch?v=OqjJjpjDRLc
Feladatsor
- A lenti lekéréseket fogalmazzuk meg relációalgebra segítségével! (ajánlott röv.: "relalg")
- A lenti lekéréseket fogalmazzuk meg sorkalkulus segítségével!
- A lenti lekéréseket fogalmazzuk meg oszlopkalkulus segítségével!
Adottak alábbi lekérésigények:
- a) Melyek az államilag nem támogatott egyetemek?
- b) Kik azok a hallgatók, akiknek nincs hallgatói jogviszonyuk államilag támogatott egyetemmel? (Feltételezzük, hogy egy hallgató egyetlen felsőoktatási intézmény diákja.)
- c) Melyek azok a szakok, amelyeket legalább két egyetemen oktatnak?
- d) Melyek azok a szakok, amiket csak egy-egy egyetemen oktatnak?
- e) Melyik a legrégebben alapított és támogatott egyetem?
Adatok:
| név | egyetem | szak | kezdés éve |
|---|---|---|---|
| Kiss Aladár | BME | informatikus | 2011 |
| Nagy Béla | BME | gépész | 2007 |
| Olaf Gergő | CEU | menedzsment | 2009 |
| Cenk Mariann | Pázmány | informatikus | 2004 |
| Takács Márton | BGE | menedzsment | 2010 |
| Rác Kata | ELTE | tanár | 2011 |
| egyetem | alapítás éve |
|---|---|
| SZTE | 1581 |
| ELTE | 1635 |
| Pázmány | 1635 |
| BGE | 1857 |
| BME | 1782 |
| név | város |
|---|---|
| Kiss Aladár | Budapest |
| Nagy Béla | Győr |
| Olaf Gergő | Pozsony |
| Cenk Mariann | Tata |
| Takács Márton | Kiskőrös |
| Rác Kata | Keszthely |
| Tóth Ödön | Budapest |
Házi feladat
Amire órán nem volt idő. Érdemes ránézni a biztonságosságot firtató feladatokra, hogy megértsétek annak is az értelmét.
Ha találtok feladatot a könyvben, megoldjátok, elküldhetitek nekem a megoldásotokat, hogy rápillantsak, jónak tűnik-e. Ide emailezz: trisz@kir-dev.hu No stress.
Következő órára az elméleti összefoglalót és/vagy a könyv 3. fejezetét olvassátok el.
Megoldások (ÚJ!)
Megjegyzés: Lesznek itt bonyolult matematikai magyarázatok, lesznek azok mellé az én konyhanyelven szült gondolataim, amik segítenek begyakorolni a kalkulussal való gondolkodást (főként a vastagon szedett kifejezések a konyhanyelven kitalált kifejezések, viszont nagyjából megfogják, mi a célja egy-egy formulának). 🧩
Fontos amúgy (mert úgy véltem felfedezni, hogy összekeveredhet a fejetekben a két dolog), hogy a sorkalkulusnak az eredménye egy sorokból álló halmaz, eredményhalmaznak is hívhatjuk. Viszont amit mi x-nek nevezünk a kifejezésekben a | karakter bal oldalán, az nem az eredményhalmaz, hanem egy-egy eleme. Matematikailag úgy olvasható minden kifejezés: „Egy x sor benne van az eredményhalmazban, ha [illeszd be ide a | karakter másik oldalán lévő kifejezést].” Például az első kifejezésnél lentebb: „Egy x sor benne van az eredményhalmazban, ha létezik olyan u 2 oszlopos dolog, ami benne van Á relációban ÉS ennek az u-nak az 1. oszlopának értéke azonos a vizsgált x 1. oszlopának értékével.” Így pl.: ha az x pl. [ Cirmos ], akkor az nincs benne az eredményhalmazban, mert nem találnánk olyan u 2 oszlopos dolgot, ami benne lenne Á-ban és még Cirmos lenne az 1. oszlopának értéke. Viszont ha x pl. [ BME ] lenne, akkor az már okés, mert találunk egy u 2 oszlopos dolgot (pl. [ BME, 1782 ]) ami benne van az Á-ban, és még a BME-vel azonos lesz az 1. oszlopának értéke. 👌
a) Melyek az államilag nem támogatott egyetemek?
Az órai megoldás 1. része:
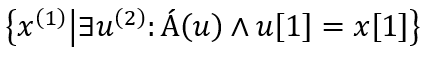
Azt mondjuk, hogy „az 1 oszlopos x lesz a megoldásunk, amibe akkor kerül érték, ha létezik legalább egy 1 oszlopos sor, ami benne van az Á táblázatban ÉS az ismeretlen x 1. oszlopa (azaz egyeteme) ennek a talált sornak az 1. oszlopával (egyetemével) legyen azonos”. Röviden még egyszer: ha van u, ami Á-beli, akkor annak az egyetemét válogassuk ki.
Természetesen az órai megoldásnak csak az 1. része ez a kifejezés: ugyanis ez a kifejezés csupán kiválogatja nekünk az összes olyan sort (illetve csak az egyetemeket), ami benne van Á relációban.
Nem kellene valahova egy negálás, hogy csak eredményként olyan x-ek jöjjenek elő, amik nem az Á-ban vannak? Jól látod, viszont az Á komplementere egy végtelen nagy halmaz, amiben van KONKRÉTAN akármi (pl.: cicanevek, lakcímek, minden, ami nem Á-ban lévő 1 oszlopos sor). Úgyhogy akkor kéne nekünk egy értelmes és nagyobb halmaz, amiben ott van az összes egyetem. Ez pedig csupán a H reláció lehet, emiatt viszont tovább kell bonyolítsuk a kifejezésünket. 🛠
Az órai megoldás 2. része:
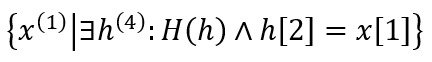
Ez sem a végső megoldást adja meg, csupán ezzel a kifejezéssel kiválogatjuk az összes olyan sort (h[2] ugye az egyetemeket jelenti, így igazából az egyetemeket válogatjuk ki), ami benne van H relációban. Ez az a fenti nagyobb halmaz.
Az órai megoldás 3. része (egyben a megoldás a kérdésre):
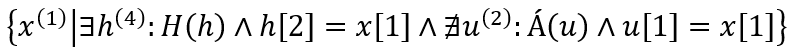
Most van az, hogy kiválogatjuk a H reláció egyetemeit, viszont azt nem engedjük, hogy az x sorok Á-beliek is legyenek. X-ek lehetnek az egyetem oszlopban felvett értékeik alapján H-beliek, viszont Á-beliek nem!
Tanulság: megismertük, hogy milyen formában lehet ilyen kiválogatásokat megírni, ahol valamely oszlop(ok) értéke(i) alapján egyezőséget keresünk (itt most az egyetem oszlop alapján csak)
b) Kik azok a hallgatók, akiknek nincs hallgatói jogviszonyuk államilag támogatott egyetemmel? (Feltételezzük, hogy egy hallgató egyetlen felsőoktatási intézmény diákja.)
Órán ez volt a megoldás:
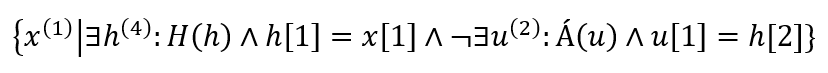
Induljunk ki egy másik megoldásból:
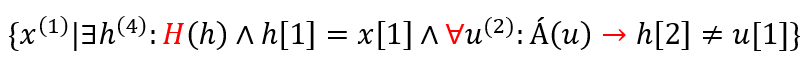
Induljunk egy ilyen gondolattal: „Kikeresem azokat a rekordokat a Hallgatók név oszlopából…”, ez az első felét mutatja, amikor olyan x-eket akarok kiszedni, amik a hallgatók neveit tartalmazzák.
Egy új kvantort használunk: univerzálisat, mert minden Á-beli u-ra szeretnénk, hogy azoknak az egyeteme ne legyen ugyanaz, mint a gyűjtött hallgatónak. Ha maradt volna az egzisztenciális, akkor csak annyit mondanánk, hogy „legyen legalább egy Á-beli u, aminek nem azonos az egyeteme az én hallgatóméval”. Ez így kevés, gondoljunk csak bele. 🧠
Eddig kb. minden mondatomat úgy kezdtem, hogy „Á-beli u”, ezért is használjuk az implikációt. Mindig vegyük számításba az implikáció lehetőségét! ☝️
Így úgy hangzik a dolog, hogy „minden 2 oszlopos u sorra legyen igaz, hogyha Á-beli, akkor viszont annak az egyeteme ne legyen azonos az én hallgatóméval”.
Kicsit fun: van egy ilyen tétel:
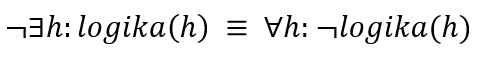
Tehát a létezikes kifejezések átírhatóak mindenes kifejezésekre, a lényeg, hogy a kvantort cserélni kell, és a kvantor jobb oldalán lévő formulát pedig tagadni kell. Levezethető, hogy a fenti adott kifejezés ugyanaz, mint az órai megoldás (először átalakítom az implikációt az egyszerűbb logikai operátorokra, aztán átalakítom a kvantort és a jobb oldalát tagadom (De Morgan-azonosság!)):
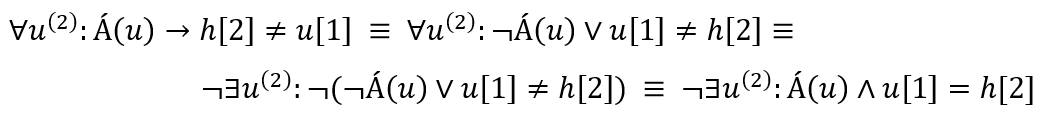
Olvasd el lentebb az implikációról szóló szemelvényt, ha többet szeretnél belőle érteni!
c) Melyek azok a szakok, amelyeket legalább két egyetemen oktatnak?
Órai megoldás:
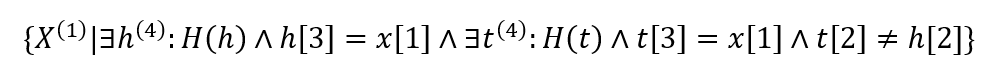
Itt azt kell igénybe vennünk, amit a relalgnál is csináltunk: ott lemásoltuk a relációt és össze Descartes-szoroztuk őket. Itt erre nincs lehetőségünk, viszont tudunk bevezetni egy arbitrális t változót, amit összhatásba tudunk hozni a h-val.
Eddig az okés, hogy t és h is H-beliek, és h-nak a szakjait szedjük ki x-ekbe. Viszont a t[3] = x[1] (= h[3]) rész a legfontosabb, ez a rész köti össze a két "létezikes" nagyobb részeket. Különben csak két különálló egzisztenciális kvantoros formulából állna az egész kifejezés, amik egymástól függetlenek. Ezzel az egyenlőséggel alakítjuk ki a kapcsolatot a két létezikes rész között. Ugyanis amíg a h-s rész feltételez csak annyit, hogy h H-beli, addig a t-s rész azt mondja, hogy a t-nek az egyeteme nem ugyanaz, mint a h-nak, de a szakja IGEN!
d) Melyek azok a szakok, amiket csak egy-egy egyetemen oktatnak?

e) Melyik a legrégebben alapított és támogatott egyetem?

Végül pedig erre a feladatra a kész oszlopkalkulusos megoldást mutatom meg, ebből könnyen megérthető, hogy formalizálandó a sorkalkulus alapján egy oszlopkalkulus kifejezés:
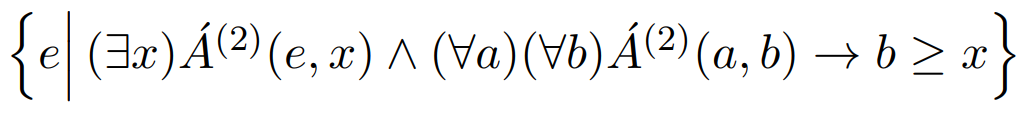
- Kicsit rövidebb a "kiválasztásos" részünk, ugyanis itt már akár az
Á(e,x)tartalmazási kritériumba be lehet illeszteni a kikeresendő egyetemek nevére való oszlopváltozót. - Itt már nem egy N-es sorra kell az univerzális kvantort (
∀) használni, hanem egyes oszlopokra, és így indexelésre sincs szükség. - Házi feladatként próbáld meg magadnak átalakítani a többi sorkalkulusodat is oszlopkalkulusra, hogy a kezed is megszokja a formalizálás módszerét.
A → B
A gyakorlaton és itt a megoldások között is gyakran használom az implikációt (→ karakterrel jelölt logikai operátor). A dolog BSZ1/2-ből, Analízisből lehet ismert, mint amikor egy tételt fogalmazunk meg, pl.: Ha egy egyszerű gráf síkba rajzolható, akkor 4 színnel színezhető. Ezt a tételt ha kicsit átírjuk: { G gráf síkba rajzolható } → { G gráf 4 színezhető }. A mondat két oldalán egy-egy logikai kifejezés van, amik igazak vagy hamisak lehetnek.
Érdemes lehet megnézni, hogy milyen is a A → B logikai formula igazságtáblája:
| A | B | A → B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Fentiekből megállapíthatjuk, hogy a A → B logikai formula megegyezik a ¬A v B (azaz (NOT A) OR B) formulával, amit habár könnyebb megjegyezni, attól még tök jól jöhet az implikáció operátora, hiszen könnyebb vele szavakban kifejezni, amit akarunk: "ha a h sor H-beli, akkor még muszáj a h[1]-nek x[1]-gyel egyenlőnek lenni (egyébként eldobjuk)" stb.
Ami még fontos lehet az implikációval kapcsolatosan, hogy nem szabad összetéveszteni az ekvivalenciával (↔), mert az oda-vissza működik, nem csak oda! Az ekvivalenciát matematikában általában az "akkor és csak akkor, ha..." vagy "pontosan akkor, ha..." mondatrészekkel szokás kifejezni, míg a sima implikációt egyszerűen a "ha ..., akkor ..." formában tudjuk megfogalmazni. Példa az ekvivalencia fogalmazásmódjára: Egy összefüggő gráfban akkor és csak akkor létezik Euler-kör, ha minden csúcsának fokszáma páros, máshogy írva: { G összefüggő gráf, minden csúcsának fokszáma páros } ↔ { G gráfban létezik Euler-kör }.